Nama : IRNA MARLIANA SIREGAR
Kelas : Pagi
Jurusan : Informatika
1. Konsep kapasitansi elektrostatik dalam bidang fisika.
Sejarah kelistrikan diawali dengan diamatinya bahan ambar atau resin yang dalam bahasa Yunani berarti Elektron,
yang apabila bahan tersebut digosok dengan kulit binatang berambut akan
dapat menarik benda–benda halus yang ringan yang setelah menempel
padanya lalu ditolaknya.
Sifat demikian ternyata tertularkan pada benda lain yang disinggungkan
atau yang ditempelkan padanya,
yang oleh karenanya benda itu lalu dikatakan bermuatan “keambaran” atau resinious.
Hal yang sama ternyata terjadi pula pada kaca yang digosok dengan kain
sutera, yang penularannya menjadikan benda lain yang ditempelkan padanya
bermuatan “kekacaan” atau vitrious.
Pada tahun 1733, Francois du Fay menemukan kenyataan bahwa
di alam hanya ada dua jenis muatan saja, yaitu muatan resinious dan
vitrious, dan dua benda yang muatannya sama akan tolak–menolak dan
sebaliknya dua benda akan tarik–menarik jika muatannya berbeda.
Kemudian Benjamin Franklin (1706–1790)
menemukan kenyataan bahwa dua jenis muatan resinious dan vitrious itu
kalau digabungkan akan saling meniadakan seperti halnya dengan bilangan
positif dan negatif. Sejak itu muatan resinious disebut muatan listrik
negatif dan vitrious disebut dengan muatan listrik positif.
Melanjutkan percobaan Michelson dan Carlisle tentang elektrolisa, Michael Faraday (1791–1867)
pada tahun 1883 mengemukakan terkuantisasinya muatan listrik menjadi
unit–unit muatan, yang kemudian oleh Stoney pada tahun 1874, yang
diperkuat oleh J.J. Thomson pada tahun 1897,
dihipotesiskan adanya partikel pembawa muatan listrik yang lalu
dinamakan elekron. Sebagai resin, elektron dikatakan menghasilkan muatan
listrik negatif maka elektron pun akan bermuatan listrik negatif.
Hukum Coulomb
Meskipun J.C. Maxwell (1831-1879) berhasil memadukan semua hukum dan rumus kelistrikan dalam bentuk empat persamaan yang lalu dikenal sebagai persamaan maxwell
sedemikian hingga semua gejala kelistrikan selalu dapat diterangkan
berdasarkan atau dijabarkan dari keempat persamaan itu, pada hakikatnya
keempat persamaan itu dapat dipadukan menjadi atau dapat dijabarkan dari
hukum Coulomb:
 yakni yang menyatakan bahwa gaya antara dua muatan listrik
q1 dan q2 akan sebanding dengan banyaknya muatan listrik masing–masing
serta berbanding terbalik dengan kuadrat jarak (r) antara kedua muatan
listrik tersebut, serta tergantung pada medium di mana kedua muatan itu
berada, yang dalam perumusannya ditetapkan oleh suatu tetapan medium k.
Jadi hukum Coulomb merupakan hukum yang fundamental dalam ilmu
kelistrikan, yang mendasari semua hukum dan rumus kelistrikan, seperti
halnya hukum 'inisial Newton' dalam mekanika yang mendasari semua hukum
dan rumus mekanika.
Dalam sistem satuan m.k.s, tetapan medium k tertuliskan sebagai
1/(4 π ε ), sehingga hukum Coulomb menjadi berbentuk:
yakni yang menyatakan bahwa gaya antara dua muatan listrik
q1 dan q2 akan sebanding dengan banyaknya muatan listrik masing–masing
serta berbanding terbalik dengan kuadrat jarak (r) antara kedua muatan
listrik tersebut, serta tergantung pada medium di mana kedua muatan itu
berada, yang dalam perumusannya ditetapkan oleh suatu tetapan medium k.
Jadi hukum Coulomb merupakan hukum yang fundamental dalam ilmu
kelistrikan, yang mendasari semua hukum dan rumus kelistrikan, seperti
halnya hukum 'inisial Newton' dalam mekanika yang mendasari semua hukum
dan rumus mekanika.
Dalam sistem satuan m.k.s, tetapan medium k tertuliskan sebagai
1/(4 π ε ), sehingga hukum Coulomb menjadi berbentuk:
 dan ε disebut permitivitas medium.
Dengan F positif berarti gaya itu tolak-menolak dan sebaliknya F negatif berarti tarik–menarik.
dan ε disebut permitivitas medium.
Dengan F positif berarti gaya itu tolak-menolak dan sebaliknya F negatif berarti tarik–menarik.
Medan Listrik
Adanya
muatan listrik di dalam ruang akan menyebabkan setiap muatan listrik
yang ada di dalam ruangan itu mengalami gaya elektrostatis Coulomb,
yaitu yang menurutkan hukum Coulomb di atas. Oleh sebab itu dikatakan
bahwa muatan listrik akan menimbulkan medan listrik disekitarnya. Medan
listrik dikatakan kuat apabila gaya pada muatan listrik di dalam ruangan
bermedan listrik itu besar. Tetapi gaya coulomb itu besar terhadap
muatan listrik yang banyak sehingga didefinisikan kuat medan listrik
sebagai gaya pada satu satuan muatan listrik. Jadi dari hukum Coulomb di
atas, kuat medan listrik oleh titik muatan listrik q adalah:

Di mana r ialah vektor satuan arah radial dari titik muatan q .
Sebagaimana gaya adalah besaran vektor maka begitu juga kuat medan listrik  sehingga kuat medan listrik oleh beberapa titik muatan listrik q1, q2,
q3, … sama dengan jumlah vektor–vektor kuat medan listrik oleh
masing–masing titik muatan listrik, yaitu:
sehingga kuat medan listrik oleh beberapa titik muatan listrik q1, q2,
q3, … sama dengan jumlah vektor–vektor kuat medan listrik oleh
masing–masing titik muatan listrik, yaitu:

Garis Gaya Medan Listrik
Garis
gaya medan listrik bukanlah besaran nyata melainkan suatu abstraksi
atau angan–angan atau gambaran yang menyatakan arah medan listrik di
berbagai tempat di dalam ruang bermedan listrik, yakni yang polanya
menyatakan distribusi arah medan listrik. Arah medan listrik setempat,
yaitu pada arah garis gaya di tempat itu, sudah tentu menyinggung garis
gaya di tempat tersebut.
Pada hakikatnya memang setiap titik pasti dilalui suatu garis gaya,
sehingga garis–garis gaya akan memenuhi seluruh ruangan. Tetapi
seandainya semua garis gaya kita gambarkan, maka sistem pola garis dari
gaya itu tidak akan tampak. Oleh sebab itu banyak garis gaya yang
dilukis harus dibatasi, misalnya sebanyak muatan yang memancarkannya;
artinya, banyak garis gaya yang digambarkan, yang memancar dari titik
muatan listrik q adalah juga sebanya q saja, agar pola sistem garis gaya
itu tampak dan memiliki makna, yang kecuali menyatakan distribusi arah
medan listrik juga memperlihatkan distribusi kuat medan listrik di mana
yang bagian garis gayanya rapat, medan listriknya juga rapat.
Untuk medan listrik oleh titik muatan q, menurut hukum coulomb, kuat
medan listriknya berbanding terbalik dengan kuadrat jaraknya. Tetapi
dengan melukis sebanyak q garis gaya yang memancarkan radial merata dari
titik muatan q, suatu permukaan bola berjari–jari r yang berpusat di q
akan ditembus tegak lurus leh flux garis gaya  yang sebanyak q, yakni
yang sebanyak q, yakni  sama dengan q, sehingga rapat garis gaya yang didefinisikan sebagai
banyaknya garis gaya yang menembus suatu satuan luas permukaan tegak
lurus pada permukaan bola itu diberikan oleh:
sama dengan q, sehingga rapat garis gaya yang didefinisikan sebagai
banyaknya garis gaya yang menembus suatu satuan luas permukaan tegak
lurus pada permukaan bola itu diberikan oleh:
 dengan D yang disebut induksi elektrik. Jadi induksi elektrik setempat
diberikan oleh rapat flux garis gaya medan listrik di tempat itu yaitu:
dengan D yang disebut induksi elektrik. Jadi induksi elektrik setempat
diberikan oleh rapat flux garis gaya medan listrik di tempat itu yaitu:  Yang berarti kuat medan listrik setempat sebanding dengan rapat flux
garis gaya medan listrik di tempat itu.
Dengan definisi serta pengertian garis gaya medan listrik seperti yang
diutarakan di atas, maka garis gaya tersebut memiliki sifat–sifat
sebagai berikut:
Yang berarti kuat medan listrik setempat sebanding dengan rapat flux
garis gaya medan listrik di tempat itu.
Dengan definisi serta pengertian garis gaya medan listrik seperti yang
diutarakan di atas, maka garis gaya tersebut memiliki sifat–sifat
sebagai berikut:
- Tidak berpotongan satu sama lain, sebab arah medan listrik setempat adalah pasti.
- Kontinu, sebab medan listrik ada di setiap titik di dalam ruang.
- Seolah–olah ditolak oleh muatan positif dan sebaliknya ditarik oleh muatan negatif.
- Dipotong tegak lurus oleh bidang–bidang equipotensial sebab usaha
yang dilakukan satu satuan muatan listrik dari sutu titik ke titik lain
di bidang equipotensial adalah nol karena tidak ada perubahan tenaga
potensial, yang harus berarti arah gaya medannya, yaitu arah garis gaya
medannya, selalu tegak lurus bidang equipotensial tersebut.
Potensial Listrik
Sejalan
dengan tenaga potensial dalam mekanika, potensial listrik didefinisikan
sebagai yang sedemikian hingga turunnya tenaga potensial dari suatu
titik A ke titik B sama dengan usaha yang dilakukan oleh satu satuan
muatan listrik selama bergerak dari A ke B.
Untuk medan listrik yang oleh satu titik muatan q turunnya potensial
listrik itu menjadi:
 yang dengan mengambil VB = 0 untuk rB =
yang dengan mengambil VB = 0 untuk rB =  ,
yakni dengan menyatakan potensial listrik itu di tempat yang jauh tak
terhingga dari q adalah nol, sejalan dengan tiadanya potensi untuk
melakukan usaha sebab kuat medan listrik E di r =
,
yakni dengan menyatakan potensial listrik itu di tempat yang jauh tak
terhingga dari q adalah nol, sejalan dengan tiadanya potensi untuk
melakukan usaha sebab kuat medan listrik E di r =  adalah nol, kita dapat merumuskan potensial listrik oleh titik muatan
listrik q di tempat sejauh r dari titik muatan itu sebagai:
adalah nol, kita dapat merumuskan potensial listrik oleh titik muatan
listrik q di tempat sejauh r dari titik muatan itu sebagai:
 yang sama dengan usaha yang sama dengan oleh satu satuan muatan listrik
yang bergerak dari tempat sejauh r dari q, ke tempat tak terhingga
jauhnya dari q, atau dapat juga dikatakan sama dengan usaha yang
diperlukan untuk mengambil satu satuan muatan listrik dari tempat jauh
tak terhingga ke tempat sejauh r dari titik muatan q.
Selanjutnya didefinisikanlah satuan potensial volt. Jikalau usaha yang
dilakukan oleh 1 coulomb muatan listrik adalah 1 joule maka turunan
potensial adalah 1 volt, di mana muatan listrik satu coulomb adalah yang
pada pemindahannya dalam pengendapan elektrolit mengendapkan 1,118
miligram Ag dari larutan elektrolit AgNO3. jelaslah bahwa untuk Q
coulomb muatan yang melintasi benda potensial V volt, diperlukan usaha
sebesar QV joule yang berarti coulomb Volt = joule.
Lebih lanjut, dalam hukum Coulomb, satuan permitivitas medium adalah
yang sedemikian hingga apabila satuan untuk muatan listrik q
adalah coulomb dan satuan untuk jarak adalah meter, maka satuan untuk
gaya elektrostatika Coulomb adalah Newton. Jadi untuk satuan
permitivitas medium itu ialah coulomb2/ (newton meter)
Sejalan dengan yang berlaku dalam mekanika di mana gaya F = - gradien
potensial, maka dalam elektrostatika juga berlaku hubungan kuat medan
listrik E = - gradien potensial listrik V atau dirumuskan:
yang sama dengan usaha yang sama dengan oleh satu satuan muatan listrik
yang bergerak dari tempat sejauh r dari q, ke tempat tak terhingga
jauhnya dari q, atau dapat juga dikatakan sama dengan usaha yang
diperlukan untuk mengambil satu satuan muatan listrik dari tempat jauh
tak terhingga ke tempat sejauh r dari titik muatan q.
Selanjutnya didefinisikanlah satuan potensial volt. Jikalau usaha yang
dilakukan oleh 1 coulomb muatan listrik adalah 1 joule maka turunan
potensial adalah 1 volt, di mana muatan listrik satu coulomb adalah yang
pada pemindahannya dalam pengendapan elektrolit mengendapkan 1,118
miligram Ag dari larutan elektrolit AgNO3. jelaslah bahwa untuk Q
coulomb muatan yang melintasi benda potensial V volt, diperlukan usaha
sebesar QV joule yang berarti coulomb Volt = joule.
Lebih lanjut, dalam hukum Coulomb, satuan permitivitas medium adalah
yang sedemikian hingga apabila satuan untuk muatan listrik q
adalah coulomb dan satuan untuk jarak adalah meter, maka satuan untuk
gaya elektrostatika Coulomb adalah Newton. Jadi untuk satuan
permitivitas medium itu ialah coulomb2/ (newton meter)
Sejalan dengan yang berlaku dalam mekanika di mana gaya F = - gradien
potensial, maka dalam elektrostatika juga berlaku hubungan kuat medan
listrik E = - gradien potensial listrik V atau dirumuskan:
 ]
Di mana
]
Di mana
 ialah operator deferensial vektor nabla Laplace, yaitu:
ialah operator deferensial vektor nabla Laplace, yaitu:
 Dengan i, j, k, adalah vektor–vektor satuan panjang sumbu–sumbu koordinat X, Y, Z di dalam sisitem koordinat cartesius.
Dengan i, j, k, adalah vektor–vektor satuan panjang sumbu–sumbu koordinat X, Y, Z di dalam sisitem koordinat cartesius.
Tenaga Sistem Titik-titik Muatan Listrik
Yang
dimaksud dengan tenaga sistem atau himpunan titik–titik muatan listrik
di sini ialah tenaga yang diperlukan untuk menghimpun ataupun tenaga
yang dikandung sistem titik–titik muatan listrik tersebut, yang adalah
sama dengan usaha yang dilakukan oleh titik–titik muatan itu seandainya
dibiarkan berserakan menuju jauh tak terhingga. Untuk menjelaskan
penjabaran rumusnya, kita perhatikan Gambar 1.3 yang memeperlihatkan
himpunan titik–titik muatan q1 yang berada di tempat potensial V1, q2 di
tempat potensial listrik V2 dan seterusnya.
U1 = 0
U2 = q2V21
U3 = q3V31 + q3V32
U4 = q4V41 + q4V42 + q4V43
U = U1 + U2 + U3 + U4
Misalkan penghimpunan titik–titik muatan itu kita mulai dengan mengambil
titik muatan q1 dari tempat jauh tak terhingga. Untuk ini tidak perlu
melakukan usaha, sebab tidak ada tidak ada medan listrik yang harus
diatasinya. Tetapi untuk mengambil q2 dari tempat jauh tak terhingga ke
tempatnya yang diperlukan usaha karena diperlukan gaya untuk mengatasi
medan listrik yang ditimbulkan oleh q1 dan usaha itu adalah sebesar U2 =
q2V21 di mana V21 adalah potensial listrik di tempat q2 karena adanya
muatan listrik q1, demikian seterusnya secara umum kita dapat menulis:
 dan
dan  Di mana U adalah tenaga sistem yang dimaksud.
Adapun potensial listrik di tempat qi diberikan oleh jumlah yang ada pada masing–masing muatan lainnya, yaitu:
Di mana U adalah tenaga sistem yang dimaksud.
Adapun potensial listrik di tempat qi diberikan oleh jumlah yang ada pada masing–masing muatan lainnya, yaitu:
 Di lain pihak qiVij = qjVji
Di lain pihak qiVij = qjVji
Elektrostatika Untuk Terapi
Yang
dimaksud dengan elektrostatika untuk terapi adalah efek yang
ditimbulkan oleh keberadaan muatan listrik, yang statis (tidak
berubah/bergerak) seperti elektron, ion, atau proton, dalam ruangan yang
ada di sekitarnya dengan tegangan 9000 Volt yang bisa digunakan untuk
kesehatan (Terapi Medan Elektrostatis). Secara sederhana energi
elektrostatis dapat dihasilkan dengan menggosok dua buah isolator. Gaya
elektrostatis yang timbul dapat menarik potongan kertas atau rambut
berdiri. Terapi elektrostatis merupakan terapi yang dapat menciptakan
tekanan seimbang ion dalam tubuh, terutama zat ion (ion postasium,
sodium, magnesium, kalsium, dll.) dalam tubuh yang akan membuat tubuh
menjadi lebih rileks. Terapi ini menggunakan tegangan listrik sebesar
9000 Volt dengan getaran 50x/detik (frekuensi 50 Hz) yang akan mampu
untuk menggetarkan kotoran-kotoran yang menggumpal dan menempel pada
dinding-dinding pembuluh darah, sehingga akan merontokkannya secara
perlahan-lahan dan dalam kurun waktu 1 minggu dengan terapi 1 jam per 1
kali terapi untuk keluhan hipertensi akan berkurang atau bahkan sembuh
dengan mengembalikan elastisitas pembuluh darah dengan vibrilasi yang
timbul akibat stimulus listrik dengan menjadikan ruptur plak dalam
pembuluh darah serta energi panas yang memvasodilatasi pembuluh darah.
Manfaat dari terapi medan elektrostatis ini antara lain membersihkan
saluran darah, dengan getaran 50x/detik dengan tegangan listrik 9000
volt yang akan dikeluarkan melalui saluran pembuangan kita yaitu: urine,
keringat dan juga kotoran (BAB), meningkatkan daya tahan tubuh,
menambahkan Ion negatif dalam tubuh, membuang sel yang tidak baik (sel
yang sudah mati), mempercepat pertumbuhan tulang dan mengurangi keropos
tulang, meningkatkan produksi kalsium dalam tubuh, mempertahankan PH
tubuh, menghacurkan lemak, kolesterol jahat dalam tubuh, mempercepat
pemecahan gula dalam darah, kolesterol dalam darah, menguatkan otot
jantung, fungsi paru-paru, tanpa efek samping, tanpa menggunakan
obat-obatan, dan tanpa suntikan. Biasanya penggunaan terapi medan
elektrostatis ini akan terasa khasiatnya terhadap tubuh setelah
dilakukan 7 kali atau 1 minggu. (Baik dilakukan berturut-turut ataupun
tidak)Terapi ini juga termasuk ke dalam terapi komplementer karena
selain menstabilkan ion tubuh, medan magnet yang ditimbulkan oleh terapi
ini akan bervibrasi sehingga timbul panas. Terkait materi selengkapnya
ada dalam Biolistrik.
Kapasitansi Konduktor
Yang
dimaksud dengan kapasitansi adalah ukuran kapasitas, yakni kemampuan
menampung muatan listrik. Suatu konduktor kalau dimuati muatan listrik
akan menjadi bermedan listrik di permukaannya, namun muatan listrik yang
ada padanya tidak ditolak keluar dan lepas dari konduktor sebab gaya
medan elektrostatis itu diimbangi oleh gaya tarik muatan listrik yang
tandanya berlawanan yang berasal dari atom–atom konduktor itu sendiri.
Akan tetapi bilamana muatan listriknya terlalu banyak maka medan listrik
yang ditimbulkannya akan menjadi kuat sehingga daya tarik dari
atom–atom konduktor tidak lagi mampu mengatasi gaya tolak keluar
konduktor. Akibatnya sebagian muatan listrik yang dimuatkan padanya
menjadi lepas kembali karena konduktor itu tidak mampu menampung muatan
listrik lebih lanjut.
Demikianlah hubungan kesebandingan antara kuat medan listrik di
permukaan konduktor dengan banyaknya muatan listrik yang dimuatkan ke
konduktor tersebut, begitu pula antara potensial listrik konduktor itu
dengan banyaknya muatan listrik yang dimuatkan.
Untuk merumuskan secara konkret, terlebih dahulu kita pelajari sifat
konduktor yang berkaitan dengan kuat medan listrik di permukaannya yang
disebabkan oleh muatan listrik yang ada padanya.
- Definisi Konduktor
Secara ekstrem, demi mudahnya pembahasan yang kita maksud dengan
konduktor ialah bahan yang mengantarkan listrik dengan sempurna; yang
berarti bahwa muatan listrik yang dimuatkan padanya akan bebas bergerak
tanpa hambatan sedikitpun. Dengan definisi yang demikian maka konduktor
memiliki sifat–sifat sebagai berikut:
- Muatan listrik yang dimuatkan akan ada di permukaan
Hal ini dengan mudah dapat dijelaskan berdasarkan gaya tolak–menolak
di antara muatan–muatan listrik yang dimuatkan sehingga akan sejauh
mungkin saling menjauhi, tetapi masih belum lepas keluar dari permukaan
konduktor.
- Arah medan listrik di permukaan adalah tegak lurus dari permukaan itu
Seandainya arah medan listrik di permukaan itu miring terhadap
permukaan, maka muatan listrik yang ada di permukaan akan mengalami gaya
medan karena adanya komponen medan listrik sepanjang arah yang
menyinggung permukaan. Jadi dalam keadaan setimbang komponen medan
listrik yang pada arah mendatar adalah nol, yang berarti medan listrik
di permukaan konduktor pasti arahnya tegak lurus permukaan.
- Di dalam konduktor tidak ada medan listrik
Dengan menerapkan theorema Gauss dengan integrasi yang mencakup
permukaan tepat di bawah permukaan konduktor seperti dijelaskan oleh bagian c nilai integral itu adalah nol karena tidak
bermuatan listrik sama sekali mengingat seluruh muatan listrik yang
dimuatkan ada di permukaan konduktor. Seandainya di dalam konduktor itu
ada distribusi arah medan listrik, tentunya arahnya entah semua keluar
entah semua masuk ke permukaan, sehingga nilai integralnya tidak sama
dengan nol. Jadi nilai integral nol harus berarti bahwa kuat medan
listrik nol yakni di sembarang tempat dalam konduktor.
- Konduktor adalah benda equipotensial
Karena tidak ada muatan listrik di dalam konduktor maka tidak
diperlukan usaha untuk memindahkan listrik dari titik A ke titik B di
dalam konduktor, yang berarti potensial listrik di A sama dengan yang
ada di B juga tidak diperlukan usaha untuk memindahkan muatan listrik
sembarang titik di permukaan konduktor ke titik lainnya yang juga ada di
permukaan konduktor sebab arah medan listrik di permukaan konduktor
tegak lurus dengan permukaan. Jadi potensial listrik di semua titik di
permukaan konduktor adalah sama dan juga sama dengan yang ada dalam
konduktor. Dengan kata lain konduktor merupakan benda equipotensial;
maksudnya potensial listriknya sama di mana–mana di dalam maupun di
permukaan konduktor.
- Muatan listrik yang dimuatkan ke konduktor berongga akan ada di permukaan luarnya saja
Dengan pertolongan Gambar 2.1 bagian e kita amati bahwa dengan
menerapkan theorema Gauss dengan integrasi yang meliputi luasan di
antara rongga konduktor di dalam konduktor, nilai integral itu pasti
sama dengan nol sebab kuat medan listrik dalam konduktor di mana–mana
adalah nol, yang berarti bahwa luasan integrasi itu tidak mencakup
muatan listrik, yang berarti pula tidak ada muatan listrik di permukaan
rongga. Muatan listrik yang dimuatkan seluruhnya akan ada di permukaan
luar.
- Kuat medan listrik di permukaan konduktor sebanding dengan rapat medan di tempat itu
Dengan pertolongan bagian f kita amati bahwa dengan
menerapkan theorema Gauss yang meliputi ke enam dinding segi empat, yang
memberi kontribusi pada integrasi hanyalah permukaan atas saja karena
hanya permukaan itu yang ditembus garis gaya. Seandainya luas permukaan
itu adalah A, maka nilai integral Gauss itu adalah E.A yang harus sama
dengan total muatan listrik yang tercakup dalam permitivitas medium,
yaitu  q. A bila
q. A bila  q adalah rapat muatan listrik di permukaan yang luasnya sudut tentu juga.
q adalah rapat muatan listrik di permukaan yang luasnya sudut tentu juga.
2. Konsep dielektrik elektrostatik dalam bidang fisika.
Dielektrik adalah sejenis bahan Isolator listrik yang dapat dikutubkan (polarized) dengan cara menempatkan bahan dielektrik dalam medan listrik.
Ketika bahan ini berada dalam medan listrik, muatan listrik yang
terkandung di dalamnya tidak akan mengalir, sehingga tidak timbul arus
seperti bahan konduktor, tetapi hanya sedikit bergeser dari posisi setimbangnya mengakibatkan terciptanya pengutuban dielektrik.
Oleh karena pengutuban dielektrik, muatan positif bergerak menuju kutub
negatif medan listrik, sedang muatan negatif bergerak pada arah
berlawanan (yaitu menuju kutub positif medan listrik) Hal ini
menimbulkan medan listrik internal (di dalam bahan dielektrik) yang
menyebabkan jumlah keseluruhan medan listrik yang melingkupi bahan
dielektrik menurun. Jika bahan dielektrik terdiri dari molekul-molekul yang memiliki ikatan
lemah, molekul-molekul ini tidak hanya menjadi terkutub, tetapi juga
sampai bisa tertata ulang sehingga sumbu simetrinya mengikuti arah medan
listrik.
Walaupun istilah "isolator" juga mengandung arti konduksi listriknya
rendah, seperti "dielektrik", tetapi istilah "dielektrik" biasanya
digunakan untuk bahan-bahan isolator yang memiliki tingkat kemampuan
pengutuban tinggi yang besarannya diwakili oleh konstanta dielektrik. Contoh umum tentang dielektrik adalah sekat isolator di antara plat konduktor yang terdapat dalam kapasitor. Pengutuban bahan dielektrik dengan memaparkan medan listrik padanya mengubah muatan listrik pada kutub-kutub kapasitor.
Penelitian tentang sifat-sifat bahan dielektrik berhubungan erat
dengan kemampuannya menyimpan dan melepaskan energi listrik dan
magnetik. Sifat-sifat dielektrik sangat penting untuk menjelaskan berbagai fenomena dalam bidan elektronika, optika, dan fisika zat padat.
Istilah "dielektrik" pertama kali dipergunakan oleh
William Whewell (dari kata "dia" dari yunani yang berarti "lewat" dan "elektrik") sebagai jawaban atas permintaan dari
Michael Faraday.
Kerentanan kelistrikan (Susceptibility)
Kerentanan kelistrikan Xe pada bahan dielektrik adalah ukuran seberapa mudah bahan ini dikutubkan dalam medan listrik, yang pada akhirnya menentukan permitivitas listrik sehingga mempengaruhi sifat-sifat lain dalam bahan dielektrik tersebut, misalnya nilai kapasitansi jika dipergunakan dalam kapasitor.
nilai kerentanan listrik ini didefinisikan melalui sebuah konstanta perbandingan antara medan listrik E dan pengkutuban bahan dielektrik P sedemikian rupa sehingga:

di mana  adalah Permitivitas ruang hampa.
adalah Permitivitas ruang hampa.
Kerentanan sebuah bahan memiliki hubungan dengan permitivitas relatifnya  yaitu:
yaitu:

Sehingga dalam ruang hampa,

Perpindahan medan listrik D berhubungan dengan kerapatan pengkutuban P melalui:

Penyebaran (dispersi) dan hukum sebab-akibat
Secara umum, sebuah bahan tidak dapat langsung terkutub (polarized) secara mendadak pada saat berada dalam medan listrik. Bentuk umum rumus sebagai fungsi waktu pengutuban ini adalah:

Artinya pengkutuban terjadi sebagai bentuk pembelokan (konvolusi) terhadap medan listrik pada masa lampau (waktu sebelumnya) dengan nilai kerentanan listrik saat ini yang bernilai  . Batas atas dari integral ini dapat terus diperpanjang sampai tak terhingga karena
. Batas atas dari integral ini dapat terus diperpanjang sampai tak terhingga karena  untuk
untuk  . Respon pengutuban mendadak dapat terjadi karena Fungsi delta dirac dengan kerentanan
. Respon pengutuban mendadak dapat terjadi karena Fungsi delta dirac dengan kerentanan  .
.
Namun perhitungan menjadi lebih mudah dalam sistem linear jika menggunakan rumus Transformasi Fourier dan menulis persamaan ini sebagai fungsi frekuensi. Karena adanya teorema konvolusi, bentuk integral berubah menjadi perkalian sederhana,

Perlu diperhatikan bahwa frekuensi sederhada ini bergantung pada
nilai kerentanan, atau nilai permitivitas. Bentuk grafik kerentanan
berdasar frekuensi ini memberi sifat dispersi pada bahan dielektrik.
Lebih jauh, bahwa pengutuban hanya bergantung pada medan listrik pada waktu lampau (yaitu  untuk
untuk  ), sebagai konsekuensi atas hukum sebab-akibat, pengutuban memiliki hubungan Kramers–Kronig pada kerentanan
), sebagai konsekuensi atas hukum sebab-akibat, pengutuban memiliki hubungan Kramers–Kronig pada kerentanan  .
.
Pengutuban dielektrik
Permodelan atom sederhana
Interaksi medan listrik dengan permodelan
atom dielektrik klasik.
Dalam pendekatan teori klasik tentang permodelan dielektrik, sebuah bahan terbuat dari atom-atom. Tiap atom terdiri dari awan bermuatan negatif (elektron)
terikat dan meliputi titik bermuatan positif di tengahnya. Dengan
keberadaan medan listrik disekeliling atom ini maka awan bermuatan
negatif tersebut berubah bentuk, seperti yang terlihat pada gambar yang
atas-kanan .
Hal ini dapat dipandang secara sederhana sebagai dwikutub (dipole) dengan menggunakan prinsip-prinsip superposisi. Dwikutub ini dicirikan oleh momen dwikutubnya, yaitu besaran vektor yang ditampilkan pada gambar sebagai panah biru dengan tanda M.
Yang berperan membentuk perilaku dielektrik adalah Hubungan antara
medan listrik dan momen dwikutubnya. (Catatan bahwa pada gambar momen
dwikutub digambarkan mengarah pada arah yang sama dengan medan listrik,
hal ini tidak selalu benar-benar terjadi, dan ini hanya merupakan
penyederhanaan saja, tetapi penggambaran seperti ini biasanya masih
sesuai untuk berbagai bahan.)
Ketika medan listrik hilang, atom-atom pada bahan tersebut
kembali pada keadaan sebelumnya. Waktu yang diperlukan untuk
berubah-ubah keadaan ini disebut waktu Relaksasi; grafiknya berbentuk penurunan secara ekponensial.
Permodelan di atas merupakan penggambaran sederhana saja, pada
praktiknya perilaku dielektrik sangat bergantung pada situasinya. Makin
rumit situasinya (membutuhkan akurasi lebih) makin rumit pula permodelan
yang harus dibuat untuk menjelaskan perilaku bahan dielektrik secara
akrat. Permasalahan paling mendasar adalah:
- Apakah medan listrik dalam bahan tersebut konstan ataukah berubah sejalan waktu?
- Jika berubah sejalan waktu, seberapa besar perubahannya?
- Bagaimana ciri-ciri bahan tersebut?
- Apakah arah medan listrik merupakan isotropi yang penting?
- Apakah bahan tersebut homogen?
- Adakah batasan-batasan yang harus diperhatikan?
- Apakah harus diperhatikan bila sistemnya linear atau nonlinear?
Hubungan antara medan listrik E dan momen dwikutub M mempengaruhi perilaku bahan dielektrik, yang mana pada bahan tertentu, dapat dicirikan melalui fungsi F dengan persamaan:
 .
.
Ketika medan listrik dan jenis bahan telah ditentukan, lalu ditentukan fungsi F paling sederhana untuk mendapatkan hasil paling mendekati dari sifat yang diinginkan.
Pengutuban dwikutub
Pengutuban dwikutub (dipole polarization) adalah pengutuban pada kutub-kutub molekulnya. Pengutuban jenis ini berakibat pengutuban secara permanen, contohnya ikatan asimetris antara atom oksigen dan hidrogen pada air,
yang akan mempertahankan sifat-sifat pengutuban walaupun medan listrik
sudah hilang. Pengutuban jenis ini membentuk pengutuban makroskopis.
Jika medan listrik dari luar dipaparkan pada bahan tertentu, jarak antara muatan dalam atom, yang terkait dengan ikatan kimianya, tidak berubah selama terkutub; namun, kutub-kutubnya akan berputar. Putarannya tergantung pada torsi dan viskositas
molekul yang bersangkutan. Karena perputaran ini tidak dapat terjadi
secara mendadak, pengutuban dwikutub belum terjadi ketika frekuensi
pengutuban masih rendah. Jarak waktu respon muatan listrik karena adanya
medan listrik ini menimbulkan gesekan dan panas.
Pengutuban ion
Pengutuban ion adalah pengutuban yang terjadi karena adanya perpindahan relatif antara ion negatif dan positif dalam molekul yang bersangkutan, misalnya pada NaCl). Sering kristal atau molekul tidak terdiri hanya satu jenis atom
saja, distribusi muatan listrik disekitar atom kristal atau molekul
cenderung positif atau negatif. Akibatnya, ketika getaran molekul
menginduksi perpindahan muatan dalam atom, titik setimbang muatan
positif dan negatif mungkin tidak berada pada lokasi yang sama. Titik
setimbang ini mempengaruhi simetri sebaran muatan listrik. Ketika titik
setimbang ini tidak setimbang, pengkutuban terjadi dalam kristal atau
molekul tersebut. Inilah pengutuban ion.
Pengutuban ion menyebabkan transisi feroelektrik dan juga pengutuban dwipolar. Transisi yang disebabkan berubahnya urutan arah kutub permanen sepanjang garis tertentu, disebut transisi fase order-disorder. Sedang transisi yang disebabkan oleh pengutuban ion dalam kristal disebut transisi fase pergeseran.
Dispersi dielektrik
Dalam ilmu fisika, dispersi dielektrik
adalah ketergantungan bahan dielektrik pada nilai permitivitasnya pada
frekuensi tertentu ketika adanya medan listrik. Karena adanya jeda waktu
antara pengutuban dan perubahan medan listrik, permitivitas bahan
dielektrik menjadi sangat rumit, diperlukan fungsi dengan bilangan kompleks dari frekuensi medan listrik. Hal ini sangat penting dalam penggunaan bahan dielektrik dan analisis sistem pengutuban.
Kejadian umum atas fenomena ini disebut sebagai dispersi bahan: yaitu respon yang tergantung pada frekuensi dari suatu bahan untuk menghantarkan gelombang (wave propagation).
Ketika frekuensi meningkat:
- Pengutuban dwikutub tidak mungkin mengejar perubahan medan listrik ketika memasuki daeran gelombang mikro sekitar 1010 Hz;
- Ketika memasuki daerah infra-merah atau infra-merah-jauh sekitar 1013 Hz, pengutuban ion tidak lagi merespon terhadap medan listrik;
- Pengutuban listrik benar-benar tidak mungkin terjadi ketika frekuensi memasuki daerah ultraungu sekitar 1015 Hz.
Dalam frekuensi di atas ultraungu, permitivitas mendekati nilai konstanta ε0 untuk semua bahan, di mana ε0
adalah permitivitas ruang hampa. Karena permitivitas merupakan kekuatan
hubungan antara medan listrik dan pengutuban, jika pengutuban tidak
lagi merespon medan listrik, maka permitivitas menurun.
Relaksasi dielektrik
Relaksasi dielektrik adalah komponen jeda waktu dalam konstanta dielektrik suatu bahan. Jeda ini biasanya disebabkan oleh jeda waktu yang diperlukan molekul bahan sampai terkutub (polarized) ketika mengalami perubahan medan listrik disekitar bahan dielektrik (misalnya, kapasitor yang dialiri arus listrik). Relaksasi dielektrik ketika terjadi perubahan medan listrik dapat dipersamakan dengan adanya histerisis ketika terjadi perubahan medan magnet (dalam induktor atau transformer). Dalam sistem linier,
relaksasi secara umum berarti jeda waktu sebelum respon yang diinginkan
muncul, oleh karena itu relaksasi diukur sebagai nilai relatif terhadap
keadaan dielektrik stabil yang diharapkan (equilibrium). Jeda waktu antara munculnya medan listrik dan terjadinya pengutuban berakibat berkurangnya energi bebas (G) tanpa dapat dikembalikan.
Dalam ilmu fisika, relaksasi dielektrik
mengacu pada waktu respon relaksasi bahan dielektrik atas medan listrik
dari luar pada frekuensi gelombang mikro. Relaksasi ini sering
diterangkan dalam permitivitas sebagai fungsi terhadap frekuensi,
yang mana, dalam sistem ideal, dapat dinyatakan dalam persamaan Debye.
Namun di lain pihak, pergeseran pengutuban ion dan pengutuban elektron
menunjukkan perilaku sejenis resonansi atau osilasi. Ciri proses pergeseran sangat bergantung pada struktur, komposisi, dan lingkungan sekitar dari bahan.
Jumlah panjang gelombang yang bisa dipancarkan sebagai radiasi
ketika terjadinya relaksasi dielektrik dapat ditemukan menggunakan Hukum
Hemmings yang pertama

di mana
- n adalah jumlah panjang gelombang yang bisa dipancarkan sebagai radiasi
 adalah jumlah tingkat energi.
adalah jumlah tingkat energi.
Relaksasi Debye
Relaksasi Debye
adalah respon relaksasi dari sekumpulan dwikutub yang tak berinteraksi
satu sama lain, secara ideal, atas berubahnya medan listrik dari luar.
Biasanya nilainya dinyatakan sebagai permitivitas kompleks  dari bahan sebagai fungsi terhadap frekuensi medan listrik
dari bahan sebagai fungsi terhadap frekuensi medan listrik  :
:

di mana  adalah permitivitas pada batas frekuensi tertinggi,
adalah permitivitas pada batas frekuensi tertinggi,  di mana
di mana  merupakan permitivitas statis berfrekuensi rendah, dan
merupakan permitivitas statis berfrekuensi rendah, dan  adalah ciri waktu relaksasi dari bahan yang bersangkutan.
adalah ciri waktu relaksasi dari bahan yang bersangkutan.
Model relaksasi seperti ini pertama kali diperkenalkan (dan dinamai sesuai yang memperkenalkan) oleh Peter Debye pada tahun 1913.
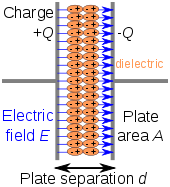
Kapasitor
Pemisahan muatan listrik dalam lempengan
konduktor sejajar menimbulkan medan listrik internal. Bahan dielektrik (oranye) mengurangi medan internal sambil menambah
kapasitansi.
Kapasitor yang diproduksi untuk komersial biasanya menggunakan bahan dielektrik padat
yang memiliki permitivitas tinggi sebagai pemisah antara muatan positif
dan negatif yang disimpan. Bahan ini sering pula disebut sebagai
"dielektrik kapasitor".
Keuntungan yang jelas terlihat jika menggunakan bahan dielektrik
semacam ini adalah mencegah dua plat konduktor yang mana terdapat muatan
listrik saling berhubungan langsung. Dan yang lebih penting,
permitivitas tinggi memungkinkan lebih banyak muatan listrik yang
tersimpan pada potensial yang sama. Kerapatan muatan listrik σε yang bisa disimpan jika menggunakan bahan dielektrik linear dengan permitivitas ε dan ketebalan d untuk memisah dua konduktor dapat dihitung dengan

dan kapasitansi per satuan luas adalah

Dari sini, bisa kita lihat bahwa semakin besar ε makin besar pula muatan yang disimpan (σε) dan akhirnya makin besar pula nilai kapasitansinya. Bahan dielektrik yang digunakan dalam kapasitor juga dipilih yang sulit terionisasi
agar kapasitor dapat dipergunakan pada potensial tinggi tanpa khawatir
bahan dielektrik terionisasi dan mengalirkan arus (arus bocor).
Resonator dielektrik
Osilator resonator dielektrik (DRO -- Dielectric Resonator Oscillator) adalah komponen elektronika yang menghasilkan resonansi dalam rentang frekuensi sempit, biasanya pada pita gelombang mikro. Komponen ini terdiri dari "puck" keramik yang memiliki konstanta dielektrik besar dan faktor lesapan (dissipation factor)
rendah. Resonator semacam ini digunakan untuk mendapatkan frekuensi
acuan dalam rangkaian osilator. Resonator dielektrik tak-terlindung (unshielded) dapat ditemui pada Antena Resonator Dielektrik (DRA -- Dielectric Resonator Antenna).
Dielektrik dalam praktik
Bahan dielektrik dapat berupa zat padat, zat cair, atau gas.
Bahkan, ruang hampa-pun dapat dianggap bahan dielektrik walaupun
konstanta dielektrik relatifnya merupakan identitas (bernilai 1). Tampaknya dielektrik dalam bentuk padat lebih umum dipergunakan dalam ilmu kelistrikan, dan banyak zat padat merupakan isolator yang baik. Beberapa contoh antara lain porselen, kaca, dan sebagian besar plastik. Udara, nitrogen, dan belerang hexafluoride adalah tiga gas yang umum digunakan sebagai bahan dielektrik.
- Pelapis industrial seperti parylene bertindak sebagai penghalang dielektrik antara bahan yang dilapisi dan lingkungan sekitar.
- Minyak yang digunakan dalam transformer
(terutama yang besar) berguna sebagai bahan dielektrik cair dan sebagai
pendingin. Bahan dielektrik cair memiliki konstanta dielektrik yang
lebih tinggi, sehingga bisa dipergunakan dalam kapasitor tegangan tinggi sehingga mencegah terjadinya muatan bocor bila terjadi korona dan juga meningkatkan nilai kapasitansi.
- Karena bahan dielektrik menghambat arus listrik, permukaan bahan dielektrik bisa saja menangkap muatan listrik berlebih yang terlepas. Hal ini dapat terjadi secara tidak sengaja ketika bahan dielektrik tergesek atau tersentuh bahan lain sehingga terjadi efek tribolistrik. Namun kadang kala kejadian seperti ini justru diinginkan seperti dalam generator Van De Graff atau elektroforus, atau dapat pula kejadian ini malah merusak seperti dalam pelepasan listrik statis.
- Bahan dielektrik khusus yang disebut elektret dapat menyimpan muatan listrik cukup lama, hampir seperti magnet yang mampu menyimpan medan magnet.
- Beberapa bahan dielektrik mampu menghasilkan potensial listrik ketika mengalami tekanan, atau dapat berubah bentuk ketika diberi potensi listrik. Sifat ini disebut sebagai sifat piezoelektrik. Bahan piezoelektrik merupakan jenis dielektrik yang sangat berguna dalam berbagai alat.
- Beberapa bahan dielektrik dalam bentuk kristal ion dan polimer memiliki momen dwikutub sendiri, yang dapat dimodifikasi oleh medan listrik dari luar. Perilaku ini disebut efek feroelektrik. Bahan-bahan ini berperilaku seperti bahan feromagnetik
ketika terpapar medan magnet. Bahan feroelektrik sering kali memiliki
konstanta dielektrik yang sangat besar, sehingga bahan-bahan jenis ini
sangat berguna dalam pembuatan kapasitor.
3. Energi Elektrostatik.
Energi potensial listrik, atau energi potensial elektrostatik, adalah energi potensial (diukur dalam joule) yang dihasilkan dari gaya-gaya Coulomb konservatif dan diasosiasikan dengan konfigurasi sejumlah muatan-muatan titik dalam sebuah sistem yang didefinisikan. Suatu objek dapat memiliki energi potensial listrik karena dua elemen utama: muatan listriknya sendiri dan posisi relatifnya terhadap objek bermuatan listrik lainnya.
Satuan.